Grupos y códigos
CODIFICACIÓN DE INFORMACIÓN BINARIA
SISTEMA DE NUMERACIÓN BINARIO
De lo anteriormente presentado, podemos concluir que un sistema de numeración es un conjunto de reglas y símbolos que permiten representar datos de forma numérica.
El sistema binario (cuyos orígenes datan del siglo III A.C.), en informática y ciencias de la computación es un sistema de numeración en el que los números son representados utilizando únicamente ceros y unos, debido a que las computadoras trabajan electrónicamente con dos niveles de voltaje.
El código binario es usado para la representación y procesamiento de la información a nivel informático y de telecomunicaciones, dicha información viene dada por una cadena de bits y generalmente suele presentarse en tablas en notación octal, decimal o hexadecimal.

CONVERSIÓN ENTRE BINARIO Y DECIMAL
- De decimal a binario: para hacer la conversión de decimal a binario, hay que ir dividiendo el número decimal entre dos y anotar en una columna a la derecha el resto (un 0 si el resultado de la división es par y un 1 si es impar). La lista de ceros y unos leídos de abajo a arriba es el resultado.
- De binario a decimal: para realizar la conversión de binario a decimal, trabajaremos los números de derecha a izquierda y asignándoles de manera creciente una potencia de 2, iniciando en 2^0. Finalmente, los resultados de las operaciones realizadas se sumarán y obtendremos el número decimal.
CODIFICACIÓN Y DETECCIÓN DE ERRORES
- Se elige un entero n > m y una función uno a uno e La función e es una función de codificación (m, n) y es vista como un medio para representar cada palabra codificada. Los ceros y unos adicionales pueden proporcionar el medio para detectar o corregir los errores producidos en el canal de transmisión.
- Se transmite la palabra codificada a través de un canal de transmisión.
CORRECCIÓN DE ERRORES
La detección y corrección de errores es una importante práctica para el mantenimiento e integridad de los datos a través de diferentes procedimientos.
Se puede tratar de dos formas, cuando se detecta el error en un determinado fragmento de datos, el receptor solicita al emisor la retransmisión de dicho fragmento de datos. Luego, el receptor detecta el error, y si están utilizando información redundante suficiente para aplicar el método corrector, automáticamente aplica los mecanismos necesarios para corregir dicho error.
Teóricamente es posible corregir cualquier fragmento de código binario automáticamente. Para ello, en puesto de los códigos detectores de errores utilizando los códigos correctores de errores, de mayor complejidad matemática y mayor número de bits redundantes necesarios. La necesidad de mayor número de bits redundantes hace que a veces la corrección de múltiples bits sea inviable e ineficiente por el elevado número de bits necesarios. Por ello normalmente los códigos correctores de error se reducen a la corrección de 1,2 o 3 bits.
CÓDIGO HAMMING
Uno de los métodos más empleados es el código Hamming. Es un código corrector y detector de errores, desarrollado por R.W. Hamming en 1950, y se basa en los conceptos de bits redundantes y Distancia Hamming.
 detecta
detecta  -errores si dos palabras cualesquiera
-errores si dos palabras cualesquiera  que tienen una distancia de Hamming menor que
que tienen una distancia de Hamming menor que  coinciden. Dicho de otro modo, un código detecta
coinciden. Dicho de otro modo, un código detecta  -errores si y solo si la distancia de Hamming mínima entre dos palabras cualesquiera en él es a lo menos
-errores si y solo si la distancia de Hamming mínima entre dos palabras cualesquiera en él es a lo menos  .
.
 si y sólo si
si y sólo si 

d es el n.º de bits p en que son diferentes el mensaje emitido del recibido.
Si
 entonces se puede detectar un error de peso p
entonces se puede detectar un error de peso pSi
 entonces se puede corregir p dígitos.
entonces se puede corregir p dígitos.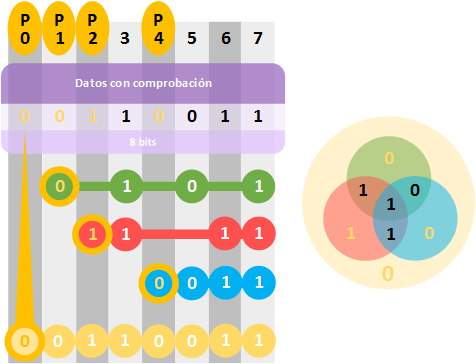








Comentarios
Publicar un comentario